الكيمياءالكيمياء العامة
طرق تعيين رتبة التفاعل Determination of Reaction Order

رتبة التفاعل Order of Reaction
** يعبر عن التغير في سرعة التفاعل مع التغير في تركيز المواد المتفاعلة بواسطة قانون فعل الكتلة. وينص هذا القانون على أنه ” تتناسب سرعة التفاعل في أي لحظة مع تركيز المواد المتفاعلة مرفوعاً إلى أس يساوي عدد جزئيات كل مادة داخلة في التفاعل فمثلاً بالنسبة للتفاعل:
A → products (1)
تتناسب سرعة التفاعل مع CA وبالنسبة للتفاعلات:
2A → products (2)
A + B → products (3)
تتناسب سرعة التفاعل مع CA2 , CA . CB على التوالي.
A + 2B → products (4)
2A + B → products (5)
تتناسب سرعة التفاعل مع CB2 , CA . CA2 . CB على التوالي.
** يتضح مما سبق أن السرعة تختلف باختلاف نوع التفاعل وعدد الجزيئات الداخلية فيه عند ثبوت درجة الحرارة. وللتمييز بين هذه التفاعلات يستعمل الاصطلاح المعروف برتبة التفاعل وتعرف رتبة التفاعل الكيميائي أنها “مجموع الأسس التي ترفع إليها تركيزات المواد المتفاعلة في معادلة السرعة” أو “عدد الجزيئات أو الذرات التي تعتمد على تركيزها سرعة التفاعل” فإذا كانت معادلة السرعة كالآتي:

حيث K هي ثابت فإن رتبة التفاعل بالنسبة للمكونات المنفردة هي :
n1 , n2 , n3 الخ ورتبة التفاعل الكلية هي:
n = n1 + n2 + n3 + ……..
وعلى هذا فأن التفاعل (1) أعلاه يسمى تفاعلاً من الرتبة الأولى والتفاعلات (2),(3) من الرتبة الثانية والتفاعلات (4) , (5) من الرتبة الثالثة.
طرق تعيين رتبة التفاعل Determination of
Reaction Order
بعد الحصول على النتائج التي تبين التغير
في التركيز مع الزمن فإن الخطوة التالية هي تعيين رتبة التفاعل بالنسبة لكل
المكونات – وفيما يلي نلخص الطرق العملية المستعملة لتعيين رتبة التفاعل:
في التركيز مع الزمن فإن الخطوة التالية هي تعيين رتبة التفاعل بالنسبة لكل
المكونات – وفيما يلي نلخص الطرق العملية المستعملة لتعيين رتبة التفاعل:
1- طريقة التكامل Method of Integration
إذا
كانت تعتمد سرعة التفاعل على تركيزات المواد المتفاعلة كما في المعادلة العامة
التالية:
كانت تعتمد سرعة التفاعل على تركيزات المواد المتفاعلة كما في المعادلة العامة
التالية:
Rate = K CAX . CBY . CCZ
فأنه
من الممكن إجراء التكامل لهذه المعادلة والحصول على إحدى المعادلات الحركية
المذكورة سابقاً وذلك حسب نوع التفاعل وتقارن هذه المعادلات التكاملية مع النتائج
لتحديد أي من هذه المعادلات تنطبق انطباقاً كاملاً مع النتائج المستخلصة عملياً
ويتم بإحدى الطريقتين الآتيتين:
من الممكن إجراء التكامل لهذه المعادلة والحصول على إحدى المعادلات الحركية
المذكورة سابقاً وذلك حسب نوع التفاعل وتقارن هذه المعادلات التكاملية مع النتائج
لتحديد أي من هذه المعادلات تنطبق انطباقاً كاملاً مع النتائج المستخلصة عملياً
ويتم بإحدى الطريقتين الآتيتين:
(أ) عددياً : تعوض النتائج العملية للتركيز مع الزمن في المعادلات التكاملية
للتفاعلات من الرتب المختلفة وذلك للحصول على ثابت السرعة، والمعادلة التي تعطي
قيماً ثابتة لهذا الثابت على مدى فترة زمنية معينة تكون هي معادلة الحركة لهذا
التفاعل وتمثل رتبته الحقيقية.
للتفاعلات من الرتب المختلفة وذلك للحصول على ثابت السرعة، والمعادلة التي تعطي
قيماً ثابتة لهذا الثابت على مدى فترة زمنية معينة تكون هي معادلة الحركة لهذا
التفاعل وتمثل رتبته الحقيقية.
مثال:
NaOC2H5+ C2H5(CH3)2SI
→ NaI + C2H5OC2H5 + S(CH3)2
→ NaI + C2H5OC2H5 + S(CH3)2
إذا
كانت A تمثل NaOC2H5 ، B تمثل C2H5(CH3)2SI فإن المعادلة الحركية تكون كالآتي:
كانت A تمثل NaOC2H5 ، B تمثل C2H5(CH3)2SI فإن المعادلة الحركية تكون كالآتي:
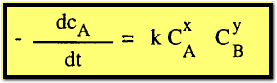
(ب) بيانياً: وتتضمن هذه الطريقة
رسم العلاقة بين التركيز والزمن بيانياً، فإذا رسم لوغاريتم التركيز مع الزمن
وأعطي خط مستقيم فإن التفاعل يعتبر من الدرجة الأولى وبالمثل بالنسبة للتفاعلات
التي تتضمن نفس التركيز الأولى من المواد المتفاعلة فإ الحصول على خط مستقيم برسم
(التركيز)-1 ،
(التركيز)-2 مع الزمن يعني أن التفاعل ثنائي الرتبة أو ثلاثي الرتبة على التوالي.
رسم العلاقة بين التركيز والزمن بيانياً، فإذا رسم لوغاريتم التركيز مع الزمن
وأعطي خط مستقيم فإن التفاعل يعتبر من الدرجة الأولى وبالمثل بالنسبة للتفاعلات
التي تتضمن نفس التركيز الأولى من المواد المتفاعلة فإ الحصول على خط مستقيم برسم
(التركيز)-1 ،
(التركيز)-2 مع الزمن يعني أن التفاعل ثنائي الرتبة أو ثلاثي الرتبة على التوالي.
ومن
مميزات طريقة التكامل أنه من الممكن حساب رتبة التفاعل بإجراء تجربة واحدة فقط.
مميزات طريقة التكامل أنه من الممكن حساب رتبة التفاعل بإجراء تجربة واحدة فقط.
2- طريقة فترة العمر الجزئية Methods
of Fractional – life
** تعرف فترة العمر الجزئية لأي تفاعل بأنه “الفترة
الزمنية اللازمة لنسبة معينة من المادة المتفاعلة لكي تستهلك” ومن أمثلتها
فترة عمر النصف t1/2 وهي الزمن اللازم لنصف كمية المادة المتفاعلة
لكي تعطي النواتج وعندها يكون تركيز المادة المتفاعلة (x) مساوياً (a/2) أي نصف التركيز الأصلي – وكذلك فإن ثلاث أرباع
العمر لأي تفاعل هو الزمن t3/4 اللازم لاستهلاك ثلاثة أرباع التركيز الأصلي
للمادة المتفاعلة. وفي هذه الحالة تكون (x = 3/4 a) .
الزمنية اللازمة لنسبة معينة من المادة المتفاعلة لكي تستهلك” ومن أمثلتها
فترة عمر النصف t1/2 وهي الزمن اللازم لنصف كمية المادة المتفاعلة
لكي تعطي النواتج وعندها يكون تركيز المادة المتفاعلة (x) مساوياً (a/2) أي نصف التركيز الأصلي – وكذلك فإن ثلاث أرباع
العمر لأي تفاعل هو الزمن t3/4 اللازم لاستهلاك ثلاثة أرباع التركيز الأصلي
للمادة المتفاعلة. وفي هذه الحالة تكون (x = 3/4 a) .
** تعتمد
فترة العمر الجزئية لأي تفاعل على رتبته، ولنفس الرتبة فإنها تعتمد على قيمة ثابت
السرعة ولتوضيح ذلك تكتب قيمة نصف العمر للتفاعلات من الرتب المختلفة.
فترة العمر الجزئية لأي تفاعل على رتبته، ولنفس الرتبة فإنها تعتمد على قيمة ثابت
السرعة ولتوضيح ذلك تكتب قيمة نصف العمر للتفاعلات من الرتب المختلفة.
في
حالة تفاعل من الرتبة الأولى:
حالة تفاعل من الرتبة الأولى:
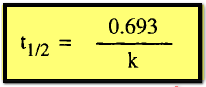
وتفاعل
من الرتبة الثانية:
من الرتبة الثانية:
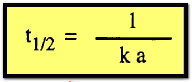
من الرتبة الثالثة:
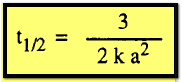
أي
أن فترة نصف العمر هي خاصية مميزة لكل تفاعل ، فهي لا تعتمد على التركيز بالنسبة
لتفاعل من الرتبة الأولى وتتناسب عكسياً مع التركيز الأولى لتفاعل من الرتبة
الثانية وعكسياً أيضاً مع مربع التركيز الأولى لتفاعل من الرتبة الثالثة وعلى هذا
فإنه يمكن كتابة معادلة عامة لتفاعل من الرتبة n كالآتي:
أن فترة نصف العمر هي خاصية مميزة لكل تفاعل ، فهي لا تعتمد على التركيز بالنسبة
لتفاعل من الرتبة الأولى وتتناسب عكسياً مع التركيز الأولى لتفاعل من الرتبة
الثانية وعكسياً أيضاً مع مربع التركيز الأولى لتفاعل من الرتبة الثالثة وعلى هذا
فإنه يمكن كتابة معادلة عامة لتفاعل من الرتبة n كالآتي:
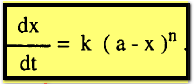
وبإجراء التكامل بين الحدود نحصل على:
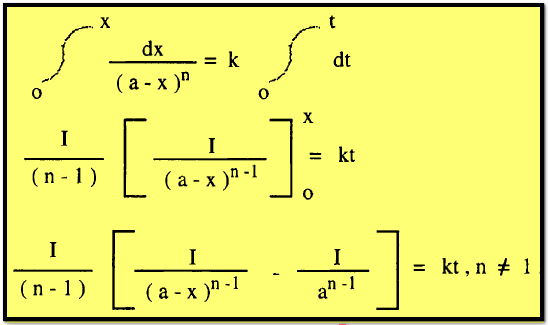
وتصلح
هذه المعادلة لجميع الرتب ماعدا الرتبة الأولى لأن (n-1) تساوي صفراً. وبالتعويض عن n بالقيم صفر ، 2 ، 3
نحصل على التوالي على معادلات التفاعلات ذات رتبة الصفر والرتبة الثانية والثالثة.
هذه المعادلة لجميع الرتب ماعدا الرتبة الأولى لأن (n-1) تساوي صفراً. وبالتعويض عن n بالقيم صفر ، 2 ، 3
نحصل على التوالي على معادلات التفاعلات ذات رتبة الصفر والرتبة الثانية والثالثة.
** وللحصول
على معادلة عامة لفترة نصف العمر عوض عن (x = a/2) فى المعادلة الأخيرة السابقة فينتج :
على معادلة عامة لفترة نصف العمر عوض عن (x = a/2) فى المعادلة الأخيرة السابقة فينتج :
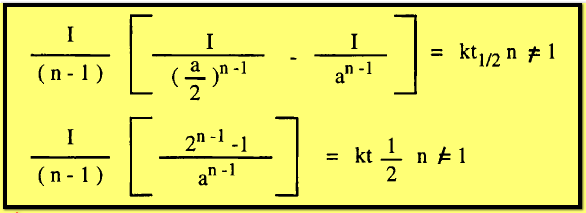
حيث
تساوي 2 ، 3 لتفاعلات من الرتبة الثانية أو الثالثة على التوالي ،
وبالتعويض بهذه القيم فى المعادلة السابقة نحصل على فترة نصف العمر في كل حالة
وبنفس الطريقة يمكن الحصول على فترة عمر جزئية.
تساوي 2 ، 3 لتفاعلات من الرتبة الثانية أو الثالثة على التوالي ،
وبالتعويض بهذه القيم فى المعادلة السابقة نحصل على فترة نصف العمر في كل حالة
وبنفس الطريقة يمكن الحصول على فترة عمر جزئية.
تعيين رتبة التفاعل باستخدام طريقة
فترة العمر الجزئية
** الزمن
اللازم لإتمام كسر معين من المواد المتفاعلة (النصف مثلاً) يعتمد على التركيز
الأولى للمواد المتفاعلة بطريقة تختلف باختلاف رتبة التفاعل .
اللازم لإتمام كسر معين من المواد المتفاعلة (النصف مثلاً) يعتمد على التركيز
الأولى للمواد المتفاعلة بطريقة تختلف باختلاف رتبة التفاعل .
**
ومن المعروف أن فترة نصف العمر t1/2 هي
الزمن اللازم لاستهلاك نصف المواد المتفاعلة. ويجب ملاحظة أن هذا الزمن لا يساوي
نصف الزمن اللازم لإتمام التفاعل وهو زمن لا نهائي إلا في حالة التفاعلات ذات رتبة
الصفر.
ومن المعروف أن فترة نصف العمر t1/2 هي
الزمن اللازم لاستهلاك نصف المواد المتفاعلة. ويجب ملاحظة أن هذا الزمن لا يساوي
نصف الزمن اللازم لإتمام التفاعل وهو زمن لا نهائي إلا في حالة التفاعلات ذات رتبة
الصفر.
**
وكما سبق معرفته من التغييرات المختلفة لقيمة t1/2 ، إذا كانت هذه القيمة تتناسب طردياً مع التركيز
الأولى فإن التفاعل يكون من الرتبة الصفرية ، وإذا كانت لا تعتمد على التركيز الأولي
فإن التفاعل يكون من الرتبة الأولى – إما إذا كانت فترة نصف العمر تتناسب عكسياً
مع التركيز الأولي أو عكسياً مع مربع التركيز الأولى فأن التفاعل يكون ثنائياً أو
ثلاثي الرتبة على الترتيب كما يتضح مما يلي:
وكما سبق معرفته من التغييرات المختلفة لقيمة t1/2 ، إذا كانت هذه القيمة تتناسب طردياً مع التركيز
الأولى فإن التفاعل يكون من الرتبة الصفرية ، وإذا كانت لا تعتمد على التركيز الأولي
فإن التفاعل يكون من الرتبة الأولى – إما إذا كانت فترة نصف العمر تتناسب عكسياً
مع التركيز الأولي أو عكسياً مع مربع التركيز الأولى فأن التفاعل يكون ثنائياً أو
ثلاثي الرتبة على الترتيب كما يتضح مما يلي:

هذا فإنه من الممكن كتابة المعادلة العامة التالية:
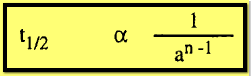
فإذا
كان التركيز الأولى فى تجربتين مختلفتين هو a ، َa والفترات المقابلة لنصف العمر هي t1/2 ، t⸌1/2 فإنه يمكن كتابة :
كان التركيز الأولى فى تجربتين مختلفتين هو a ، َa والفترات المقابلة لنصف العمر هي t1/2 ، t⸌1/2 فإنه يمكن كتابة :
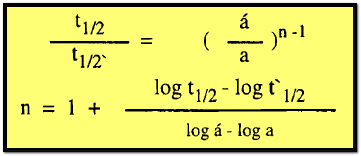
هذه المعادلة على أي فترة عمر جزئية
3- طريقة العزل Method
of Isolation
إذا
كانت المعادلة الحركية للتفاعل تتضمن أكثر من تركيز واحد فإنه من الممكن عزل واحد
أو أكثر من المواد المتفاعلة وذلك باستعمال زيادة من تركيزه. وفي هذه الحالة فإن
المادة الموجودة بتركيز كبير سوف تظل ثابتة طول التفاعل وعلى هذا فإن الرتبة
الكلية للتفاعل سوف تقل . فمثلاً فى التفاعل التالي:
كانت المعادلة الحركية للتفاعل تتضمن أكثر من تركيز واحد فإنه من الممكن عزل واحد
أو أكثر من المواد المتفاعلة وذلك باستعمال زيادة من تركيزه. وفي هذه الحالة فإن
المادة الموجودة بتركيز كبير سوف تظل ثابتة طول التفاعل وعلى هذا فإن الرتبة
الكلية للتفاعل سوف تقل . فمثلاً فى التفاعل التالي:
n1A
+ n2B + n3C→
Products
+ n2B + n3C→
Products
تكون
معادلة السرعة كالآتي:
معادلة السرعة كالآتي:
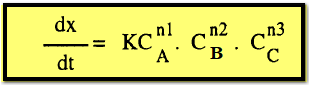
إذا
ثبت تركيز مادتين مثلاً B ، C باستعمال زيادة كبيرة منهما فإن كلاً من CBn2 ، CCn3 تظل ثابتة طول التفاعل وبالتالي تندمج في ثابت
السرعة لتعطي ثابتاً جديداً K⸌
ثبت تركيز مادتين مثلاً B ، C باستعمال زيادة كبيرة منهما فإن كلاً من CBn2 ، CCn3 تظل ثابتة طول التفاعل وبالتالي تندمج في ثابت
السرعة لتعطي ثابتاً جديداً K⸌
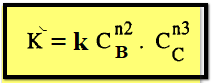
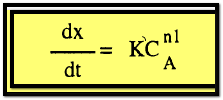
وبمعنى
هذا أن العملية من الرتبة n1 ويمكن تعيين قيمة n1 بأحدي الطرق السابقة . وتكرار هذه الطريقة يمكن
الحصول على قيمة كل من الرتب n2
, n3 وتكون الرتبة الكلية للتفاعل كالآتي :
هذا أن العملية من الرتبة n1 ويمكن تعيين قيمة n1 بأحدي الطرق السابقة . وتكرار هذه الطريقة يمكن
الحصول على قيمة كل من الرتب n2
, n3 وتكون الرتبة الكلية للتفاعل كالآتي :
n = n1 + n2 + n3
مثال: التحلل المائي للإسترات في وسط
حامضي
CH3COOC2H5 + H2O = CH3COOH
+ C2H5
+ C2H5
ويعبر
عن معادلة السرعة كالتالي :
عن معادلة السرعة كالتالي :
Rate = KCester . CH2O
وأذا
كان تركيز الماء (مذيب) موجوداً في زيادة كبيرة بالنسبة للإستر نحصل على
:
كان تركيز الماء (مذيب) موجوداً في زيادة كبيرة بالنسبة للإستر نحصل على
:
dx/dt = K⸌ . Cester
حيث K⸌ = KCH2O ويصبح التفاعل من الرتبة الأولى.
4- طريقة التفاضل Differential method
فى
هذة الطريقة التى استعملها فانته وف لا نتعامل مع المعادلات التكاملية ولكن مع
صورها التفاضلية مباشرة ومن الضروري في هذة الحالة الحصول على التغيير فى التركيز
مع التركيز الأولى وليس مع الزمن . ففى التفاعل :
هذة الطريقة التى استعملها فانته وف لا نتعامل مع المعادلات التكاملية ولكن مع
صورها التفاضلية مباشرة ومن الضروري في هذة الحالة الحصول على التغيير فى التركيز
مع التركيز الأولى وليس مع الزمن . ففى التفاعل :
n1A
+ n2B + n3C→
Products
+ n2B + n3C→
Products
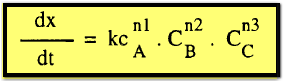
فإذا
كانت التركيزات الأولية للمواد A,B,C هي a,b,c على التوالي فإن :
كانت التركيزات الأولية للمواد A,B,C هي a,b,c على التوالي فإن :
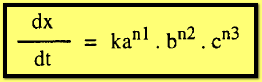
وإذا
أجرينا تجربتين ثبتنا فيهما كل من a,c وغيرنا b من b1 إلى b2 نحصل على :
أجرينا تجربتين ثبتنا فيهما كل من a,c وغيرنا b من b1 إلى b2 نحصل على :

قيمة المثبت (dx/dt) بانها تساوي النسبة بين الفروق المحددة
المقابلة لها (x/t) وبنفس الطريقة بتغيير التركيز الأولى للمادتين
الأخرتين يمكن تعيين كل من na ، nc وتكون الرتبة الكلية للتفاعل:
n = na + nb + nc
مثال
: عند اختزال أكسيد النيتريك بواسطة الهيدروجين وجد أن قيمة dp/dt تساوى 1.5 مم (ث)-1 عندما
كان الضغط الأول 152 مم وذلك بتثبيت الضغط الأول للهيدروجين . وفي تجربة أخري ثبت ضغط
أكسيد النيتريك ووجد أن قيمة dp/dt تساوى 1.6 مم (ث)-1عندما كان ضغط الهيدروجين يساوي
286 مم و 0.75 مم (ث)-1 عندما كان ضغط الهيدروجين
يساوي 147 مم ، أوجد رتبة هذا التفاعل ؟
: عند اختزال أكسيد النيتريك بواسطة الهيدروجين وجد أن قيمة dp/dt تساوى 1.5 مم (ث)-1 عندما
كان الضغط الأول 152 مم وذلك بتثبيت الضغط الأول للهيدروجين . وفي تجربة أخري ثبت ضغط
أكسيد النيتريك ووجد أن قيمة dp/dt تساوى 1.6 مم (ث)-1عندما كان ضغط الهيدروجين يساوي
286 مم و 0.75 مم (ث)-1 عندما كان ضغط الهيدروجين
يساوي 147 مم ، أوجد رتبة هذا التفاعل ؟
الحل:

إقرأ هذة الموضوعات المهمة : (أضغط على الموضوع الذي تريده)
المراجع :
– الكيمياء الحركية والكهربية.محمد مجدي عبد الله واصل ، الطبعة لأولى (1425هـ – 2004م) / دار النشر للجامعات – القاهرة – جمهورية مصر العربية






شو هي مصادركم
المراجع موجودة فى نهاية الموضوع
كيف يمكنني ايجاد الرتبة الجزئية من خلال البيان