أولاً/ إثبات قانون أفوجادرو من خلال النظرية الحركية للغازات
– أن الأحجام المتساوية للغاز تحت نفس درجة الحرارة والضغط، تحتوي أعداداً متساوية من الجزيئات. وهذا هو مبدأ أفوجادرو (قانون أفوجادرو) والذي يمكن أن نعرضه بطريقة أخري كما يلي:
( الأعداد المتساویة من جزیئات الغاز التي تشغل الحجم نفسه عند درجة الحرارة نفسھا تمارس الضغط نفسه).
– یمكن تفسیر ھذا بالإشارة إلى أن متوسط قوة الصدمة للجزیئات التي تصطدم مع مساحة معینة من الجدار تعتمد على متوسط طاقتھا الحركیة، وبالتالي على درجة حرارتھا. فإذا كانت درجتا حرارة عینتي غاز متماثلتین، عندئذ یجب أن یتساوى متوسط الطاقة الحركیة لجزیئاتھا، وإذا كان عدد الجزیئات في وحدة الحجم متماثلاً، فعندئذ، یتبع ذلك أن ضغطیھما یجب أیضاً أن یكونا متماثلین.
إثبات قانون أفوجادرو رياضيًا
نفترض أن لدينا غازين (1,2) متساویین في الحجم والضغط وطبقاً لفرض أفوجادرو فإنھما یحتویان على نفس العدد من الجزیئات ولإثبات ذلك فإن:
وبفرض تساوي الغازین في الضغط والحجم فإن:
أي أن:
وعند ثبوت درجة الحرارة للغازین، وھذا یعني أن الطاقة الحركیة لكل جزيء متساویة
وبقسمة المعادلة:
على
أي أن:
الحجوم المتساویة من الغازات المختلفة عند نفس الظروف من الضغط ودرجة الحرارة فإنھا تحتوي على نفس العدد من الجزيئات N وھذا ھو فرض أفوجادرو.
ولإثبات القانون K = V/n الناشئ من فرض أفوجادرو فإن:
وعدد الجزیئات (N) یتناسب طردیاً مع عدد المولات (n) وبالتالي فإن:
طريقة أخرى لإثبات قانون أفوجادرو
رأینا أن ضغط غاز یتناسب طردیاً مع كل من الكثافة وحرارة الغاز. وبسبب أن كتلة الغاز تتناسب طردیاً مع عدد المولات للغاز، یمكن أن نمثل الكثافة بــــ (n/V).
وعند نفس الظروف من الضغط والحجم ودرجة الحرارة:
V1 = V2 , P1 = P2 , T1 = T2
فأن:
n1 = n2
وھذا ھو التعبیر الریاضي لقانون أفوجادرو (Mathematical expression of Avogadro’s law)
ثانياً/ إثبات قانون جراهام من خلال النظرية الحركية للغازات
– یمكن استنتاج ھذا القانون مباشرة من الافتراض في نظریة الحركة بأن متوسط طاقة حركة الجزیئات تكون ثابتة بالنسبة لدرجة حرارة معینة.
– من قانون الطاقة الحركیة لجزيء:
وعندما یكون لدینا غازین (A , B)عند نفس درجة الحرارة فإن:
وحسب النظریة الحركیة التي تنص على أن الغازات عند ثبوت درجة حرارتھا فإن طاقتھا الحركیة الوسطى متساویة:
وبترتیب المعادلة الأخیرة :
وحیث أن نسبة أوزان مادتین بالجرام لبعضھما یساوى نسبة الأوزان الجزیئية نفس الغازین لبعضھما فإن:
ومن العلاقة:
نتوصل إلى قانون جراھام الآخر الذي یربط معدل الانتشار بالكثافة:
طريقة أخرى لإثبات قانون جراهام
وبما أن:
فإن:
حيث (Mw/V) الكثافة (d) ومقلوبها (V/Mw) هو مقلوب الكثافة (1/d) أي أن معدل الانتشار (r) للغاز يعتمد على سرعة الجزيئات (u) بمعنى أن الغاز الذي له أعلى معدل سرعة سوف يكون له أعلى معدل انتشار وتكون:
وعند ضغط ثابت فإن:
وھو قانون جراھام للانتشار.
ثالثاً/ إثبات قانون دالتون للضغوط الجزئية من خلال النظرية الحركية للغازات
– طبقاً لنظریة الحركة، فإنه لا یوجد قوى تجاذب (أو تنافر) ملحوظ بین الجزیئات في غاز مثالي. وفي خلیط من جزيئات غاز، كل جزيء یعمل بشكل مستقل عن الجزیئات الأخرى لذلك فإن كل جزيء يرتطم بالجدران بنفس عدد المرات لكل ثانیة، وبنفس القوة، كما لو لم یكن ھناك جزیئات أخرى موجودة. والنتیجة فإن الضغط الجزئي لغاز، لا یكون متغیراً، نتیجة لوجود غازات أخرى في الإناء الحاوي.
– إذا لم تتجاذب أو تتنافر الجزیئات فیما بینھا ، كما افترضت النظریة الحركیة، فإن الضغط الذي یعمله أي نوع من الجزئيات سوف لا یتأثر بوجود نوع آخر من الجزیئات) مثل خلیط من الغازات) وبالتالي فإن الضغط الكلي یعطى بواسطة مجموع ضغوط الغازات المفردة.
إثبات قانون دالتون رياضيًا
– إذا كان كل جزيء في غاز یتحرك مستقلاً عن أي من الجزیئات الأخرى ماعدا عند لحظة التصادم وإذا كانت التصادمات مطاطة فإنه في خلیط من غازات مختلفة سوف تكون الطاقة الحركیة الكلیة لجمیع الغازات المختلفة المكونة للخلیط الغازي مساویة لمجموع الطاقات الحركیة للغازات الفردیة، أي أن:
E = E1 + E2 + E3 + ………
– ولنعتبر لدینا خلیطاً من غازین مثالیین، تامي الامتزاج في وعاء حجمه V دون حدوث تفاعل كیمیائي بینھما من أي نوع.
فبالنسبة للغاز الأول یمكن أن نكتب العلاقة التالیة:
حیث E1 متوسط الطاقة الحركية
بالنسبة للغاز الثاني نجد أن:
وحیث أن كل جزيء یتحرك مستقلاً، فإن الضغط الذي یمارسه كل غاز على جدران الوعاء الحاوي، یمكن أن یستمد بصفة مستقلة، حیث:
والضغط الذي تمارسه إحدى مكونات الغاز یعرف بالضغط الجزئي وحیث أنه لم یحدث تفاعل بین الغازین، فإنه سوف لا یحدث تغیر في درجة حرارة الخلیط. وبالتعویض في تعبیر طاقة الخلیط:
E = E1 + E2 + E3 + ………
وبضرب طرفي المعادلة (2/3 V) نجد أن:
Ptotal = P1 + P2 + ……
وبذلك فإن الضغط الكلي (Ptotal) تساوي مجموع الضغوط الجزئیة للغازات المكونة للخلیط مھما كان عدد أنواع الغازات المكونة للخلیط مادامت لا تتفاعل كيميائياً مع بعضها.
رابعاً/ إثبات الحركة البروانية Brownian Motion من خلال النظرية الحركية
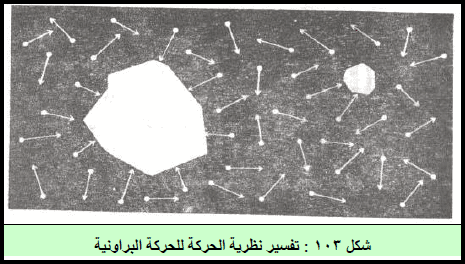
– عندما یكون جسیم معلقاً في غاز، فإن جزیئات الغاز تصطدم به. وإذا كان الجسیم كبیراً جداً، فإن عدد الجزیئات القاذفة على أحد الجوانب، یكون تقریباً مساویاً لعدد الجزیئات القاذفة bombarding على الجانب الآخر.
ولكن إذا كان الجسیم صغیراً، وبحیث أن عدد الجزیئات القاذفة في أي لحظة یكون قلیلاً، فإن الارتطامات على أحد جوانب الجسیم قد تكون غالبة، لدرجة أن الجسیم یلاقي محصلة قوة تؤدي به إلى التحرك ، ویتضح ذلك في الشكل التالي:
– ویلاحظ قرین للحركة البراونیة عندما تلقى قطعة غلیظة صغیرة من الخبز على سطح بركة یوجد بھا كثیر من السمك الصغیر. فیندفع الخبز جیئة وذھاباً ، كما لو كان مقذوفاً ببعض القوى غیر المرئیة، وترجع ھهذه القوة الخفية إلى الصراع الناتج عن السمك القاضم. وكلما كانت قطعة الخبز كبیرة، كلما كانت حركتھا الشاردة أقل.
المراجع
– أسس الكيمياء العامة والفيزيائية – الجزء الأول.عمر بن عبد الله الهزازي ، قسم الكيمياء- كلية العلوم – جامعة أم القرى – المملكة العربية السعودية
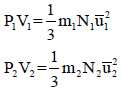
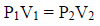
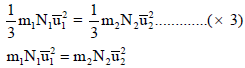
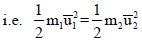
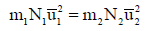
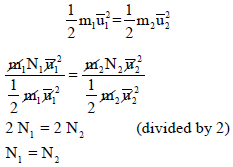
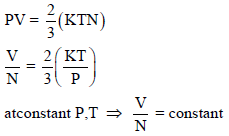
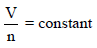
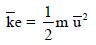
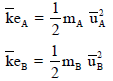
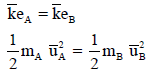
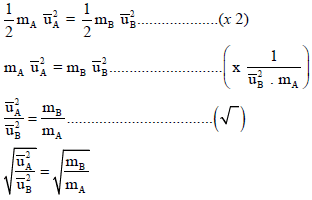
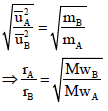
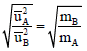
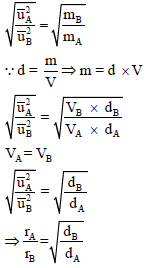
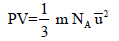
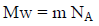
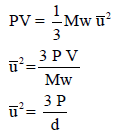
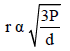
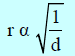
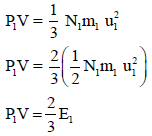
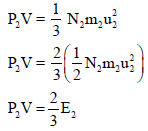
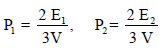
 تعرف على علم الكيمياء
تعرف على علم الكيمياء