القانون الأول للديناميكا الحرارية (قانون بقاء الطاقة)

نص القانون الأول للديناميكا الحرارية

– القانون الأول للديناميكا الحرارية First Law of Thermodynamics مرادف لقانون حفظ الطاقة ، وینص على أن:

(الطاقة لا تفنى ولا تستحدث (تخلق من عدم) ولكن یمكن فقط نقلھا من مكان الى آخر أو تحویلھا من شكل الى آخر أثناء التفاعلات أو التغیرات الكیمیائیة).

أو

(الطاقة الكلیة لنظام معزول تظل ثابتة ویمكن تحول الطاقة من صورة الى أخرى).

شرح القانون الأول للديناميكا الحرارية

– بمعنى أن طاقة النظام المعزول عن محیطه تظل ثابتة وبالتالي یمكن صیاغة القانون الأول للدینامیكا الحراریة كما یلي (الطاقة الكلیة لنظام معزول تظل ثابتة ویمكن تحول الطاقة من صورة الى أخرى).

– وھذا یعني أن مجموع كل أنواع الطاقات ثابت في أي مجموعة معزولة.

– ومن ذلك یأتي القول المعروف والقائل بأن طاقة الكون ثابتة، على أساس أن الكون یعتبر نظاماً معزولاً.

– أكبر الأثر في دعم ھذا – كان للتجارب التي أجراھا جیمس جول، حیث أثبت بتجاربه أن الحرارة والشغل المیكانیكي ھما وجھان لعملة واحدة وھي الطاقة، وأنه یمكن تحویل صور الطاقة الى بعضھا البعض، وأن الطاقة لا تفنى.

– التجارب التي تثبت أن الطاقة لا تفنى ولا تخلق من عدم، ولكنھا تتحول من صورة الى أخرى كثیرة، ومنھا: عند بذل قدر من الطاقة في ضغط لولب من الصلب، ثم إذابتة وھومضغوط في حامض، فقد یبدو أن الطاقة التي بذلت في ضغط اللولب قد فقدت، ولكن في الحقیقة إنھا اختزلت باللولب، ویؤكد ذلك أن كمیة الحرارة التي تنتج من ذوبان اللولب المضغوط، تكون أكبر من تلك التي تنتج عن ذوبان اللولب نفسه وھو غیر مضغوط. والفرق بین القیمتین یساوي مقدار الشغل المبذول في ضغط اللولب (في ھذه الحالة نجدأن الشغل قد تحول الى حرارة).

الصياغة الرياضية للقانون الأول للديناميكا الحرارية

ΔE = q + w

ΔE = مقدار التغیر في الطاقة الداخلیة للنظام

q = كمیة الحرارة الممتصة أو المنبعثة بواسطة النظام.

w = الشغل المبذول على أو بواسطة النظام.

– بعض المراجع تكتب القانون الأول في الثیرمودینامیك ریاضیاً على الصورة ΔE = q + w بدلاً من الصورة ΔE = q – w وكلاهما صحیح لأن كلاً منھم أعطى الشغل المبذول على النظام أو المبذول بواسطة النظام إشارة مخالفة.

– ففي القانون ΔE = q – w إذا كان الشغل المبذول بواسطة النظام تكون إشارته موجبة، أما إذا كان الشغل مبذولاً على النظام تكون إشارته سالبة.

– ففي القانون ΔE = q + w إذا كان الشغل المبذول بواسطة النظام تكون إشارته سالبة، أما إذا كان الشغل مبذولاً على النظام تكون إشارته موجبة.

– في المسائل الحسابية سنعتمد العلاقة:

ΔE = q + w

استنتاج القانون الأول للديناميكا الحرارية 

 یمكن للطاقة أن تنقل الى نظام ما بطریقتین أساسیتین مختلفتین كما يلي:

(1) أن یسمح للحرارة أن تنتقل داخل النظام.

(2) أن یعمل شغل على النظام.

– إذا كان لدینا نظام یتبادل الطاقة مع محیطه على شكل شغل أو طاقة حراریة، وطاقته الداخلیة الإبتدائیة تساوي (E_i) وسمحنا لكمیة من الطاقة أن تنتقل الى النظام على شكل حرارة (q)، فإن الطاقة الداخلیة للنظام تصبح كما يلي:

E_i + q

– إذا سمح أن تنتقل كمیة من الطاقة الى النظام على شكل شغل (w) فإن طاقته الداخلية عند الحالة النهائية (E_f) تكون كما يلي:

E_f = E_i + q + w

– وبترتیب العلاقة السابقة:

E_f – E_i = q + w

ΔE = q + w

ΔE = q – PΔV

والمعادلة الأخیرة:

ΔE = q + w

والتي یمكن صیاغتھا بالصورة كما يلي:

ΔE = q – PΔV

– ھي الصیغة الریاضیة المناسبة للقانون الأول للثیرمودینامیك حیث تبین تغیر الطاقة الداخلیة المرافقة لتبادل الشغل والحرارة بین النظام والمحیط.

– جدول يوضح ملخص لإشارة الشغل وكمية الحرارة كما يلي:

هل (w) ، (q) ، (ΔE) توابع للحالة (دوال حالة) ولماذا؟

– دالة الحالة هي تلك الخاصية أو الكمية التي تعتمد فقط على الحالة الابتدائية قبل التغير ، والحالة النھائیة بعد التغیر، بغض النظر عن الطریق أو المسار الذي تم من خلاله التغیر.

– الشغل (w) ، وكمية الحرارة (q) لیسا تابعین للحالة لأن كلاً منھما یعتمد على الطریق الذي یحدث خلاله التغیر، لذلك رمزنا لھما بحروف صغیرة.

– الطاقة الداخلیة (ΔE) تابعة لحالة النظام (دالة حالة) أي أنھا تعتمد على الحالة الإبتدائیة والحالة النھائیة للنظام (ولا تعتمد على المسار الذي یسلكه النظام).

الحالات الخاصة للمعادلة: ΔE = q – PΔV

(1) عند حجم ثابت Isochoric Process

– عند الحجم الثابت فإن (ΔV = 0) وبما أن العملیة تحدث دون تغیر في الحجم فإن الشغل ( w = 0) ومن ثم فإن المعادلتين:

ΔE = q – PΔV ,  ΔE = q + w

ΔV = 0 ، w = 0

ΔE = q_v

 حیث أن: q_v حرارة التفاعل عند حجم ثابت.

– وھذا یعني أن التغیر في الطاقة الداخلیة (ΔE) یكون مساویاً لكمیة الحرارة الممتصة أو المنطلقة (q).

(2) عند درجة حرارة ثابتة Isothermal Process

– وفیه تكون درجة حرارة النظام ثابتة أثناء تغیر النظام من حالة الى أخرى (ΔT = 0)، أي أن ویكون التغیر في الطاقة الداخلیة یساوي صفراً (ΔE = 0) وتؤول حینئذ المعادلتين كما يلي:

ΔE = q – PΔV ,  ΔE = q + w

ΔT = 0 ، ΔE = 0

q = – w = PΔV

– وھذا یعني أن الشغل المنجز یكون مساویاً لكمیة الحرارة.

(3) عملية مكظومة (أدياباتيكية) Adiabatic Process (نظام معزول)

– وفي ھذه الحالة لا یحدث أي تبادل حراري بین النظام والمحیط بحیث لا یضاف الى النظام ولا یؤخذ منه أي طاقة حراریة أي أن (q = 0) وبذلك تؤول المعادلتين كما يلي:

ΔE = q – PΔV ,  ΔE = q + w

q = 0

q = w = – PΔV

– وھذا یعني أن التغیر في الطاقة الداخلیة یساوي عندئذ الشغل المنجز، ویرافق ھذا النوع من العملیات تغیر في درجة الحرارة.

(4) عملية دائرية Cyclic Process

– وفي ھذه الحالة یتغیر النظام ولكنه في نھایة العملیة یرجع الى حالته الابتدائية أي أن طاقته الداخلية لا تتغیر (ΔE = 0) وبذلك تؤول المعادلتين:

ΔE = q – PΔV ,  ΔE = q + w

ΔE = 0

q = – w =  PΔV

– وھذا معناه أن الشغل یساوي كمیة الحرارة.

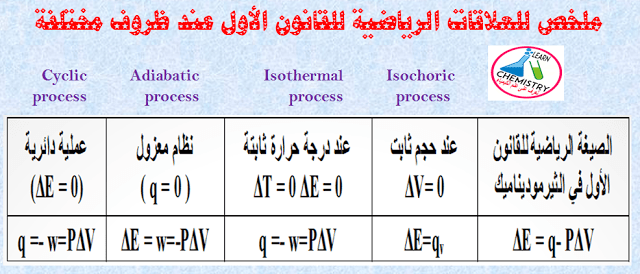
ملخص للقانون الأول للديناميكا الحرارية عند ظروف مختلفة

المراجع: أسس الكيمياء العامة والفيزيائية – الجزء الأول.عمر بن عبد الله الهزازي ، قسم الكيمياء- كلية العلوم – جامعة أم القرى – المملكة العربية السعودية.