كنا قد تناولنا في الدرس السابق شرح قانون جراهام للتدفق والانتشار Graham’s Law of Diffusion and Effusion وفى هذا الدرس نتناول مسائل محلولة كثيرة عن قانون جراهام بأفكار مختلفة فلنبدأ بإذن الله:
مسائل محلولة على قانون جراهام
مثال (1): غاز تبلغ سرعة انتشاره 1.414 مرة مقارنة بسرعة انتشار غاز SO2 عند الظروف القياسية فإذا علمت أن: (R = 0.0821 atm L/mol.K) ، (الكتل الذرية: S = 32, O = 16)
(أ) احسب الوزن الجزیئي للغاز
(ب) احسب كثافة الغاز
الحل:
(أ) حساب الوزن الجزیئي للغاز المجھول Mwx
باتباع قانون جراھام للإنتشار:
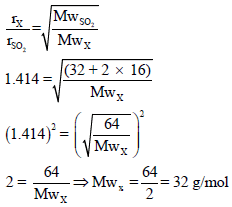
(ب) حساب كثافة الغاز بتطبیق العلاقة:
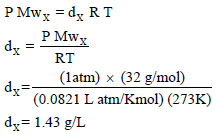
مثال (2): تدفق غاز (A) خلال ثقب ضيق في زمن قدرة 1.44 min و وتحت نفس الظروف تدفق حجم مماثل من غاز الأكسجین في زمن قدره 1.8 min احسب الكثافة النسبية للغاز (A)ووزنه الجزيئي.
الحل:
حیث أن زمن تسرب الغاز الأول (A) أقل من زمن تسرب الأكسجین، فإن كثافة الغاز (A) أقل من كثافة الأكسجین
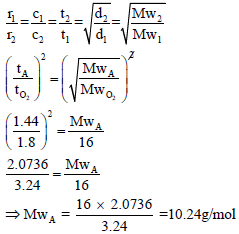
مثال (3): قارن بین كل من غازي الھیدروجین من ناحیة سرعة الإنتشار؟ علماً بأن: (MwO2 = 32 g/mol , MwH2 = 2 g/mol)
الحل:
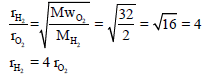
أي أن الھیدروجین أسرع انتشاراً من الأكسجین أربع مرات عند نفس الظروف
مثال (4): احسب الوزن الجزیئي لغاز ینتشر (ینساب) بسرعة 1.14 مرة أسرع من غاز الأكسجین. (الوزن الذري للأكسجین = 16)
الحل:
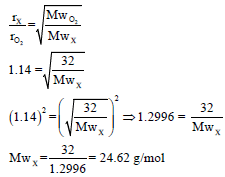
مثال (5): قارن بین غازي ثاني أكسید النیتروجین وأول أكسید النیتروجین من حیث سرعة الإنتشار؟ (الكتل الذرية: N = 14, O = 16)
الحل:
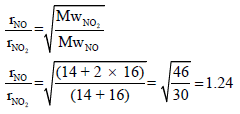
أي أن أول أكسید النیتروجین أسرع من ثاني أكسید النیتروجین بمقدار 1.24 مرة.
مثال (6): لديك غازان HBr (Mw = 81) وغاز CH4 (Mw = 16) يتسرب غاز HBr خلال فتحة صغيرة بمعدل 4 ml/s فما معدل تسرب CH4 خلال فتحة؟
الحل:
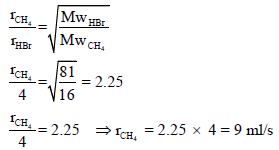
مثال (7): احسب الوزن الجزیئي لغاز إذا كان معدل انتشاره یساوي 4.69 مرة أسرع من انتشار غاز CO2 ؟ (الكتل الذرية: C = 12, O = 16)
الحل:
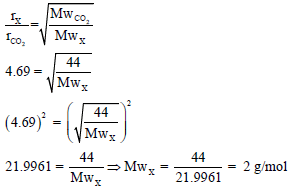
والغاز الذي وزنه الجزیئى (2)ھو غاز الھیدروجین.
مثال (8): إذا كان الوزن الجزیئي للغاز (A) ھو ضعف الوزن الجزیئي للغاز (B) فأوجدالنسبة بین معدل انتشار (A) إلى (B)؟
الحل:
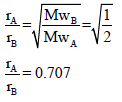
مثال (9): یحتاج مقدار من الغاز X لأن ینتشر خلال فتحة ضیقة زمن مقداره 112.25 S والزمن اللازم لانتشار نفس المقدار من O2 هو 84.7 S احسب الوزن الجزیئي للغاز. (الوزن الذري للأكسجین = 16)
الحل:
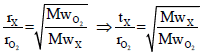
حیث أن السرعة تتناسب مع الزمن عكسیاً، وبالتالي:
مثال (10): في الأحوال القیاسیة لتر واحد من الأكسجین یزن 1.44 g بینما لتر واحد من الھیدروجین یزن (0.09 g) أي الغازین سینتشر أسرع؟ احسب كم مرة یكون أسرع؟
الحل:
نحسب أولاً الكثافة لكل غاز كما یلي:
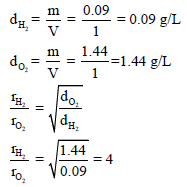
غاز (H2) ينتشر بسرعة أكبر من (O2) بأربع مرات.
مثال (11): تم تجميع (0.1 mol) من غاز مثالي فوق الماء في إناء حجمه 2.5 L حتى بلغ الضغط 745 torr فإذا علمت أن سرعة انتشار الغاز تساوي (93.5%) من سرعة انتشار غاز (N2) عند نفس الظروف فأوجد الوزن الجزيئي للغاز (N=14).
الحل:
نفرض أن سرعة انتشار الغاز (g) هي rg ، وسرعة انتشار غاز (N2) هي rN2 ومن السؤال فإن:
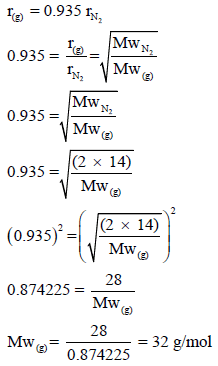
مثال (12): الزمن اللازم لانتشار حجم معین من غاز مجھول من خلال فتحة صغیرة یساوي 122.2 S الزمن اللازم لانتشار نفس الحجم من غاز الأكسجین 84.7 S احسب الوزن الجزیئي للغاز المجھول؟
الحل:
بتطبیق العلاقة التالیة:
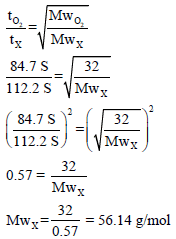
مثال (13): احسب كثافة غاز عند الظروف القیاسیة STP إذا انتشر حجم معلوم منه خلال جهاز في 5 min ، وإذا انتشر نفس الحجم من غاز الأكسجین عند نفس درجة الحرارة والضغط من خلال نفس الجھاز في زمن قدره 6.30 min (الوزن الذري للأكسجین = 16)
الحل:
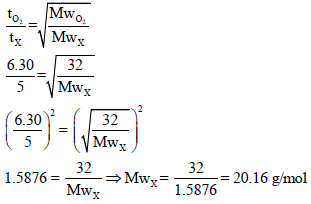
وبالتعویض بقیمة الوزن الجزیئي في العلاقة التالیة نحصل على كثافة الغاز:
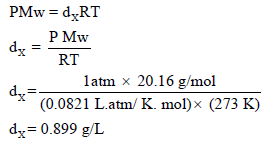
مثال (14): تبلغ كثافة غاز النیتروجین 0.572 g/L عند درجة حرارة 25Co وضغط 0.5atm ويبلغ معدل انتشار غاز النيتروجين N2 من خلال ثقب 9.50ml/S (الوزن الذري للنيتروجين =14)
(أ) ما كثافة عینة من غاز ینتشر بمعدل من خلال نفس الثقب تحت نفس الظروف؟
(ب) ما الوزن الجزیئي لھذا الغاز؟
الحل:
(أ) لحساب كثافة الغاز dX نطبق العلاقة التالیة:
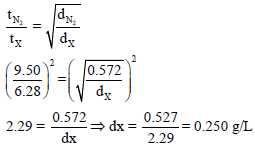
(ب) حساب الوزن الجزیئي للغاز بتطبیق العلاقة:
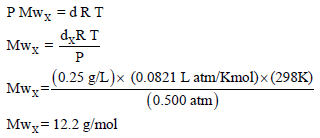
المراجع: أسس الكيمياء العامة والفيزيائية- الجزء الأول. عمر بن عبد الله الهزازي ، قسم الكيمياء- كلية العلوم – جامعة أم القرى – المملكة العربية السعودية
 تعرف على علم الكيمياء
تعرف على علم الكيمياء

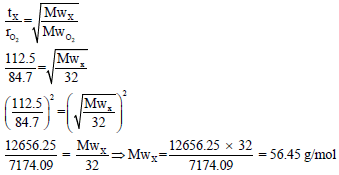




شكرا على التمرينات
تسلم شكراً على دعمك لنا
تشكر على التمرينات
Nitrogen diffuses 6times faster than gas X, the. Molar mass of X is:
a. 72
b. 36
c. 6
d.24
ضع سؤالك على موقع/ اسألني كيمياء فهو موقع تابع لنا وسوف نجيب عليك بالتفصيل