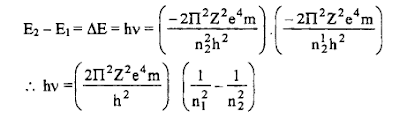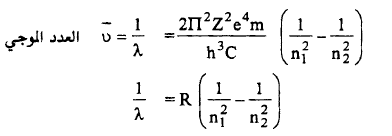– في هذا الموضوع سيتم مناقشة نظرية بور Bohr’s Theory بالتفصيل مع الشرح والمعادلات الرياضية
محتويات الموضوع
بداية نظرية بور Boher Theory
– مهد عمل اينشتاين الطريق لحل لغـز آخر في الفيزياء وهـو انبعـاث الطيـوف الذريـة.
– كمـا هـو معـروف أن الأجسـام السـاخنة المتألقـة (ضـوء سـاطع) وضـوء الشـمس جميعهـا يصـدر طيفـاً مسـتمراً تـراه العيـن المجـردة.
– تطلـق الأجسام الساخنة إلـى جانب الطيف المستمر الضوئي، طيفاً غير مرئي يسمى طيف تحت الحمراءInfrared
– أمـا طيـوف ذرات الغـاز فهـي غيـر مسـتمرة (خطـوط مضـاءة وأخـرى داكنـة) لذلـك سـمي طيفهـا بالطيـف غيـر المسـتمر لتمييـزه عـن الطيـوف المسـتمرة (الطيـف المرئـي(
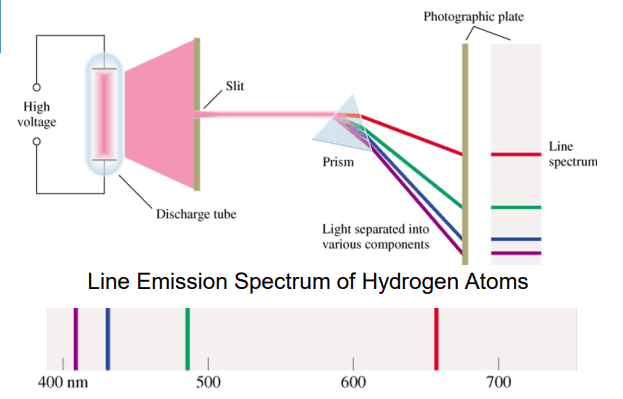
– اعتمـد بـور فـي صياغـة نظريتـه الذريـة للهيدروجيـن بشـرح طيـف ذرة الهيدروجيـن معتمـداً علـى نظريـة أن بلانك الكوانتية.
– معتبراً أن الشــعاع الصــادر عــن الهيدروجيــن الســاخن هــو نتيجــة انتقــال داخلــي لإلكترون ذرة الهيدروجين، ويطبـق أيضـاً علـى الشـعاع الصـادر مفهـوم الوحـدات الكوانتيـة.
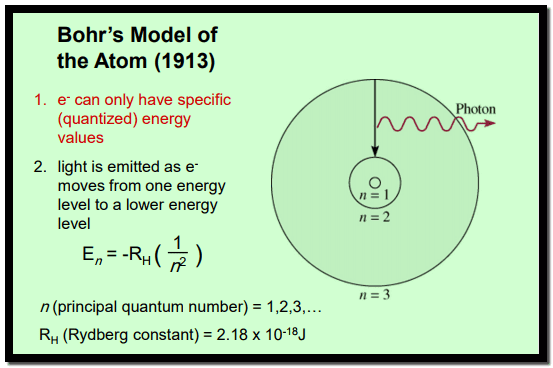
– أفترض عالم الطبيعة الدانمركي نيلز بور 1913 أن مستويات الطاقة في الذرة ترمز إلى أغلفة تدور فيها الإلكترونات الموجودة بالذرة والإلكترون الدائر في الغلاف يكون في حالة سكون (stationary state) مادامت الذرة في حالة سكون.
– بمعنى أن الذرة مادامت لا تمتص طاقة أو تشع طاقة فالإلكترون في حالة ثبات في مداره.
– وبالتالي فإن التغير في الطاقة سواء امتصت طاقة أو حدث إشعاع فأن الالكترونات تقفز من غلاف ذو طاقة سواء امتصت طاقة أو حدث إشعاع فأن الإلكترونات تقفز من غلاف ذو طاقة أقل إلى مدار ذو طاقة أعلى والعكس.
– وأضاف بور على أن الالكترونات تنتقل من مستوي الطاقة الأقل E1 إلى مستوى الطاقة آخر أعلى E2.
– وبعد فترة زمنية تعود الالكترونات إلى مدارها الأصلي وتخرج هذه الطاقة الممتصة على هيئة ضوء أو إشعاع مسببة خطوط الطيف المختلفة بحسب رقم المدار.
– ومما سبق يتضح لنا أن:
فروض نظرية بور
فروض رذرفود التى استخدمها بور
– استخدم بور بعض فروض رذرفورد عن تركيب الذرة وهي كما يلي:
فروض جديدة ابتكرها بور
– ثم أضاف بور الفروض الآتية إلى فروض رذرفورد كما يلي:
(4) في الحالة المستقرة: يبقى الإلكترون في أقل مستويات الطاقة المتاحة.
(5) في الحالة المثارة: يكتسب الإلكترون كماً من الطاقة عن طريق التسخين أو التفريغ الكهربي فينتقل مؤقتاً لمستوى طاقة أعلى) يتوقف على مقدار الكم الذي اكتسبه) ويكون الإلكترون في المستوى الأعلى في وضع غير مستقر فيعود مرة أخرى لمستواه الأصلي حيث يفقد نفس الكم من الطاقة المكتسب على هيئة إشعاع من الضوء له طول موجي و تردد مميز منتجاً طيف خطى مميز.
– وقد أضاف بوهر افتراضاً آخر ويعرف (شرط الكم) وهو العزم الدائري (Angular Momentum) وهو أن الإلكترون يدور في غلاف ثابت يساوي عدد صحيح (n) مضروباً في h/2π حيث h ثابت بلانك ، π = 22/7
العزم الدائري للإلكترون = n h / 2π (1)
– وبما أن العزم الدائري لأي جسم يتحرك في مسار دائري = الكتلة × السرعة × نصف القطر فإن:
العزم الدائري للإلكترون = m ν r (2)
حيث m = كتلة الألكترون ، v = سرعة الألكترون
– وبهذا الافتراض ومن المعادلتين (1) ، (2) أمكن حساب أماكن الخطوط الأساسية في طيف ذرة الهيدروجين.
m ν r = n h / 2π (3)
– ويعرف (n) بعدد الكم Quantum number ومن هذا المنطلق نجد أنه توجد علاقة تناسبية بين كل من (r ، n) فكلما زادت قيمة (n) زادت قيمة r.
حساب نصف قطر الأغلفة وطاقة كل منهما
– عندما يدور إلكترون في مسار دائري ذات نصف قطر (r) ينتج قوتين متساويتين في المقدار وهى قوة طرد مركزية لهذا الإلكترون وقوة جذب الكتروستاتيكية بين كل من النواة والإلكترون ومنه:
قوة الجذب الالكتروستاتيكية = قوة الطرد المركزية
Z e2 / r2= m ν2 / r
– حيث أن (Z) هي الشحنة الفعالة للنواة ومنه يمكن حساب قيمة V2
ν2 = Z e2 / m r (4)
– ومن المعادلة رقم (3) التي تم استنتاجها أعلاه:
m ν r = n h / 2π
ν = n h / 2π m r
ν2 = n2Lh2 / 4π2m2r2 (5)
– من المعادلتين (4) ، (5) نجد أن :
Ze2 / mr = n2h2 / 4π2m2r2
– ومنها يمكن حساب نصف القطر (r) من العلاقة الأتية كما يلي:
r = n2h2 / 4π2mZe2
وبالتعويض عن قيمة كل من:
Z = 1 , n =1, π = 3.14 , e = 1.6 × 10-19 coulomn , m = 9.1 ×10-28
– نجد أن قيمة نصف القطر كما يلي:
r = 0.53 Ao
– من معادلة حساب نصف القطر نجد أن أنصاف أقطار الأغلفة المتتابعة تساوى النسبة بين مربعات أرقامها كما يلي:
r1 : r2 : r3 = (1)2 : (2)2 : (3)3
حساب طاقة الإلكترون الكلية
– الطاقة الكلية عبارة عن مجموعة كلا من الطاقة الحركية 1/2 mν2 والطاقة الوضعية – Z e2 / r الناتجة عن قوي الجذب بين الإلكترون والبروتون وذلك بالنسبة لطاقة افتراضية تساوي الصفر عندما يكون الالكترون عديم الحركة وعلى مسافة لا نهائية عن النواة حتى تنعدم قوى التجاذب.
– وتتحدد الطاقة الكلية من العلاقة الآتية كما يلي:
الطاقة الكلية = طاقة الحركة + طاقة الوضع
Etotal = Ek + Ep
= 1/2 mν2 + (- Ze2 / r)
وحيث أن : mν2 = Ze2 / r
Etotal = Ze2 / 2r – Ze2 /r
= -1/2 Ze2 / r
– عندما ينتقل الإلكترون من مستوى طاقة لمستوى آخر ، فإنه يطلق فوتوناً (شعاع ضوء ذو طول موجة محدد كمومي) .
– وباستخدام المعادلة الخاصة بمستويات الطاقة للهيدروجين يمكن تحديد الأطول الموجية للضوء الذي يمكن أن ينبعث من الهيدروجين.
حساب الطاقة المنبعثة من الهيدروجين
– يتم حساب الطاقة التي تنبعث من الهيدروجين بحساب الفرق بين مستويين من مستويات طاقة الهيدروجين.
– وبالتعويض عن قيمة r = n2h2 / 4π2mZe2 فى المعادلة السابقة ينتج من ذلك المعادلة الآتية كما يلي:
وتعني الإشارة أن طاقة ذرة الهيدروجين أقل من حاصل جمع طاقتي إلكترون وبروتون مفصولين عن بعضهما بمسافة ما لانهاية ، أي أن ذرة الهيدروجين لا تتجزأ تلقائياً.
وبما أن طاقة الفوتون :
E2 – E1 = hC / λ
= 1/λ = hc (E2-E1) العدد الموجي
n1تعبر عن الحالة الأولية للإلكترون ( أي قبل لا انطلاق و لا امتصاص للطاقة(.
n2تعبر عن الحالة النهائية للإلكترون( أي بعد انطلاق أو امتصاص للطاقة(.
– وهذه المعادلة تشبه تماماً (معادلة بالمر) وبالفعل عند حساب قيمة الثابت2π2Z2e4m / h3C والتي تم الحصول عليها وجد أنها نفس القيمة للثابت ريدبرج (R)
– أن دراسـات خطـوط طيـف ذرة الهيدروجيـن وحسـابات بـور الطاقيـة المختلفـة وذلـك حسـب قيمـة n مـن 1 إلـى 4 متوافقـة مـع الطيـف المرئـي وغيـر المرئـي لـذرة الهيدروجيـن.
ΔE = hν = RH (1/n12 – 1/n22)
n1تعبر عن الحالة الأولية للإلكترون ( أي قبل الانطلاق والامتصاص للطاقة(
n2 تعبر عن الحالة النهائية للإلكترون( أي بعد انطلاق أو امتصاص للطاقة(
– عندما ينبعث الفوتون فأن n1 > n2 وعليه فإنه تكون القيمة داخل الأقواس سالبة وهذا سيؤدي إلى قيمة طاقة سالبة أى أن الطاقة تنطلق من النظام. أما عندما يتم امتصاص الطاقة n1 < n2 يصبح الحد داخل الأقواس موجباً.
– يتضمن طيف الانبعاث لذرة الهيدروجين مجموعات من الخطوط تقع في مناطق مختلفة من الطيف الكهرومغناطيسي تتراوح مابين منطقة فوق البنفسجي (متسلسلة ليمان ( Lyman series إلى المنطقة المرئية (متسلسلة بالمر series (Balmar والمنطقة تحت الحمراء (متسلسلة باشن Bachen وبراكت Brakett وفوند Pfound ).
مميزات نظرية بور
– من أهم مميزات نظرية بور المميزات الآتية كما يلي:
(1) فسرت النظرية الطيفية لذرة الهيدروجين تفسيراً صحيحاً.
(2)أول من أدخل فكرة الكم) الكوانتم (في تحديد طاقة الإلكترونات فى مستويات الطاقة المختلفة .
(3) يمكن تفسير أو تطبيق هذه الافتراضات على ذرات عناصر أخري.
– أي أنه من المتوقع أن الأغلفة (الأفلاك الإلكترونية) المرادفة تكون معقدة التركيب وهي K , L , M , N ,……. والتي بينت من قبل من خطوط الطيف لذرة الهيدروجين.
(4) أفاد بأنه يلزم لانتقال إلكترون من غلاف ذات طاقة أقل إلى غلاف آخر ذات طاقة أعلى فإنه يكتسب كمية من الطاقة أو يكتسب ذبذبات الكترومغناطيسية ذات تردد عال مكافئة لهذا المدار الجديد.
– وبالعكس إذا انتقل من أفلاك ذات طاقة أعلى إلى أفلاك ذات طاقة أدني فإنه يصحب ذلك انبعاث إشعاع.
عيوب نظرية بور
– من أهم عيوب نظرية بور العيوب الآتية كما يلي:
(1) الحسابات الكمية لنظرية بور لم تعطي النتائج المرجوة في الذرات المعقدة وحتى في ذرة الهيليوم كما هو الحال في ذرة الهيدروجين.
(2) افترض أنه يمكن تعيين كلاً من سرعة و مكان الإلكترون معاً في نفس الوقت و هذا يستحيل عملياً .
(3) استخدام قوانين الميكانيكا العادية في تفسير دوران الإلكترون.
– حيث لم تظهر أن الجسيمات في الذرة لها خواص جسيميه وكذلك خواص موجية ومن هذا المنطلق باستخدام قوانين الكم أهملت قوانين بور وهي قوانين الميكانيكا العادية.
– حيث أمكن تقدير عزم الإلكترون ، وكذلك تفسير وجود مستويات الطاقة الثابتة، كما درست أيضاً الظواهر التي تحدث في الذرة.
(4) من الدراسات السابقة لفروض بور أن ذرة الهيدروجين ما هي إلا أفلاك مسطحة في الوقت الذي ثبت فيما بعد أن الذرة لها أبعاد ثلاث في الفراغ.
(5) ظهر فيما بعد باستخدام ميكانيكا الكم أنه لا بد من وجود أربعة أنواع من الكم المختلفة.
المراجع : – أساسيات الكيمياء الفيزيائية.عبد العليم سليمان أبو المجد – فاطمة حافظ كمال محمد ، الطبعة لأولى (1426هـ – 2005م) / دار النشر للجامعات – القاهرة – جمهورية مصر العربية. – محاضرات الكيمياء العامة – الفصل الثالث – البنية الألكترونية للذرات- جامعة الأندلس الخاصة للعلوم الطبية.
 تعرف على علم الكيمياء
تعرف على علم الكيمياء